第4章 圧 密
|
 |
|
 |
4.3 圧密沈下量と圧密時間の計算
|
テルツァギ−によって提案された圧密理論を用いると、地盤の上に築造さ
れた構造物に起こる可能性がある圧密沈下量、およびその時間とともに生ず
る圧密割合を合理的に計算することができる。しかし、土は必ずしも前記模
型のような構成ではなく、また、現在の圧密理論も次のような多くの仮定に
基づいて組み立てられているので、計算の結果が、実際の場合と十分正確に
一致しないこともある。とくに、その誤差は沈下量の計算におけるものより、
時間的な進行割合の算定において著しい。
テルツァギ−の理論の中で用いられる主な仮定は、
(a)土は均質である。
(b)土の間隙は完全に水で飽和されている。
(c)土中の水は一軸的に排水され、その排水状況はダルシ−の法則に従う。
(d)土の圧縮も一軸的である。
(e)土の性質は、土の受ける圧力の大小にかかわらず変わらないものである。
(f)間隙比−圧力の関係は直線的なものである。
|
 |
|
 |
4.3.1 圧密沈下量の計算
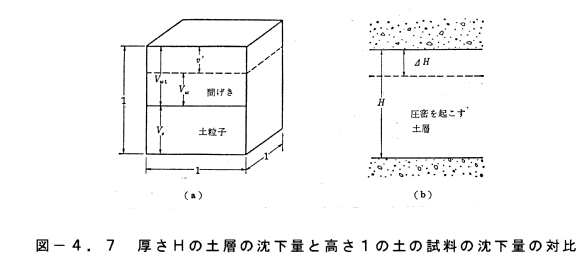
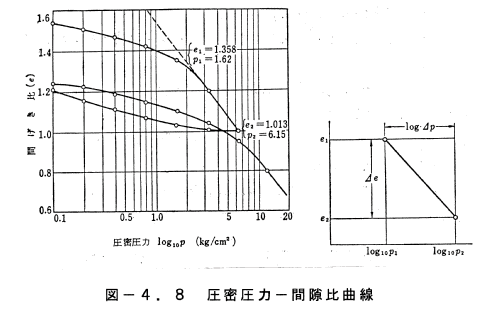
図−4.7(a)に示すような単位体積の土の試料の圧縮を、図−4.8お
よび図−4.7(b)の実際の土層と対比しながら考える。
試料の高さは1であるから、土粒子部分をVs、初めの間隙水の部分をVw1
とすると、Vw1/Vs=e1として、
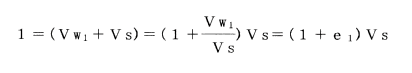
圧密後の沈下量をv'とすれば
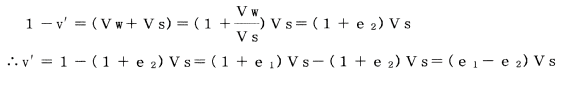
いま、土層の全層をHとすると、沈下量ΔHは、
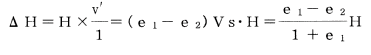
一方、e~logP曲線の直線勾配は、図—4.8(b)を参考にすると。

|
 |
|
 |
4.3.2 圧密時間
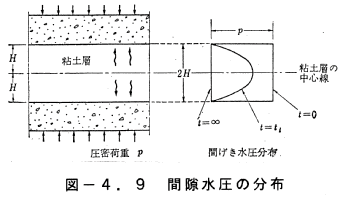
圧密の機構で述べたように、圧密は間隙水の排出に従って進行すると考え
られるから、圧密量の時間的な進行度を知るには、土層中の間隙水圧の時間
的な変化を調べなければならない。 図−4.9に示すような飽和粘土層の
間隙水が、上下に排水されるものとして、粘土層の下端からzの位置にある
微小立方体の一軸的な排水を考える。任意時刻tにおける間隙水圧をuwとし
て方程式をたてると、
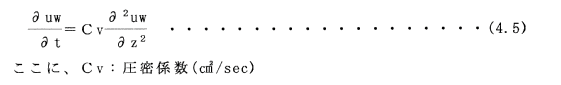
この方程式を解くと、間隙水圧は
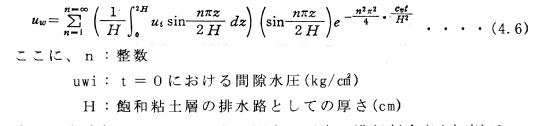
一方、任意時刻tにおける、ある深さの圧密の進行割合(圧密度)は、

このUは、圧密による最終沈下量と、圧密開始後t時間における沈下量と
の比の百分率とも定義され、次のような要素によって決まると推定される。
(1)間隙水の流速を左右する土の透水係数。
(2)土層の厚さ、および土から抜け出す水の量。
(3)水を排出させる透水面の数、および土から水が移動する距離。
(4)間隙比および圧力にともなう間隙比変化の割合、これは排水の速さと、
間隙水圧の減少の両方に関係する。
いま(4.6) 式を(4.7) 式に代入すると、

UとTvとの関係は図−4.10のようになる。UとTvとの関係は、土の
性質や圧縮量には関係がなく、土層全体を通じての応力変化や、その層に対
する排水層の数に関係するものである。
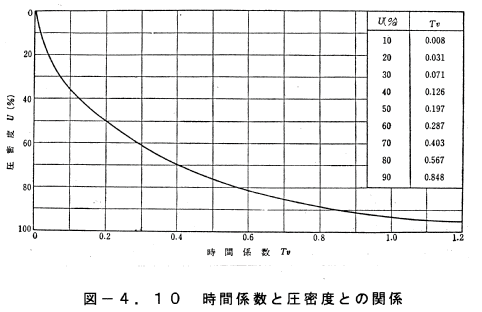
(4.4)式、(4.8)式、ならびに図−4.10に見られるように、圧密度き時
間tの指数関数を100% から減ずる形で表わされており、また粘土層の厚さ
Hの2乗に逆比例している。したがって、圧密を促進するには、なんらかの
方法で軟弱粘土層の排水経路を短くし、そして短い時間内に排水を行なうこ
とが必要である。
このような目的で、圧密を促進させる工法が数多く紹介されている。サン
ドドレ−ン工法、ペ−パ−ドレ−ン工法などは、そのようなねらいで考案さ
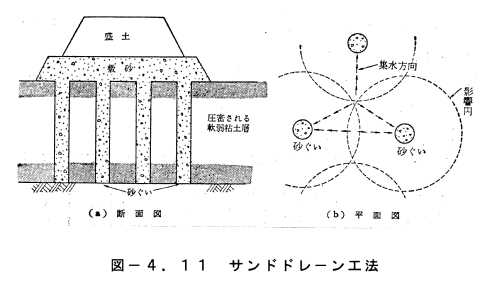
れたものである。たとえば、サンドドレ−ン工法は図−4.11(a)、(b)
のように軟弱な粘土層中に砂杭を撃ち、この砂杭に粘土中の水を水平方向に
集め、圧密を早めるものである。普通、この鉛直砂杭の上に、図(a)のよう
に敷砂をマット状に配置し、粘土層に荷重を加え、圧密すると同時に、砂杭
に集めた水を敷砂から排水させる機能も兼ねている。
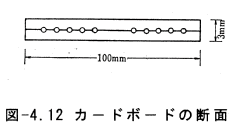
またペ−パ−ドレ−ン工法は、サンドドレ−ンの砂杭を帯状の外孔質紙(カ
−ドボ−ド)で置き換えたものと考えればよい。カ−ドボ−ドは、多数の溝
を切った紙を2枚はり合わせて作ったもので、たとえば、厚さ3mm、長さ1
0cmの図−4.12のカ−ドボ−ドは、ほぼ直径5cmの円形ドレ−ンに相
当すると考えれば、その設計方法はサンドドレ−ンとほとんど同じである。
|
 |
|
 |
4.3.3 二次圧密
過剰間隙水圧が0になった後も、層の圧密が全くやむわけではない。非常
にゆっくりした圧密が速度を減少しながら、無限に続くことが多い。これは
二次圧密と呼ばれており、土粒子相互の結合が徐々に破損するため、土粒子
構造の塑性的な再調整が行なわれる結果生ずるものと信じられている。そし
てこの塑性的再調整がまた、土粒子間に次の進行性破壊を繰り返し引き起こ
すことになる。
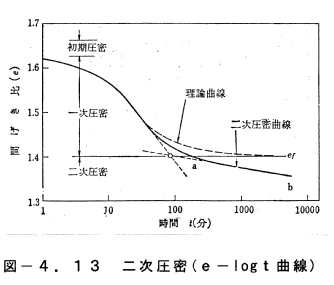
二次圧密は、沈下の様子をe−logt曲線にプロットすると、図−4.13
のような形になる。すなわち、曲線abのように、徐々に下降する比較的平
たんな直線に近いものとして表わされる。一次圧密の最終点である間隙比ef
は、図−4.13に見るように一次圧密曲線の接線と、二次圧密曲線の始点
方向への接線との交点として得られる。二次圧密の進行度は、増加荷重のΔ
pと土の圧縮特性によって決まる。
一般に低圧縮性~中圧縮性の無機質土では、二次圧密量は圧密量全体に比
べて非常に小さく、また、非常にゆっくり起こるので、普通は考えなくてよ
い。これに反し、高圧縮性の粘土・雲母を多く含む土、および有機質土の場
合は、二次圧密量はかなり大きなものとなるから、圧密の時間的な進行を圧
密理論で推定するのは難しい。
|
 |
|
 |
4.3.4 乱された土、および過圧密を受けた土の圧密
圧密に関する上記の考え方は、乱されない正規圧密を受けた粘土について
のみ正しい。乱された土および特殊な土については、各種の補正あるいは別
の考え方で対処しなければならない。
まず、乱された土については、その都度、圧密試験(4.4参照)および
必要に応じて他の土質試験も行ない、それぞれの特性を考慮して確かめる以
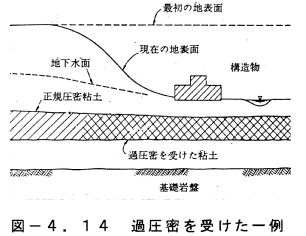
外にない。 また、過去に大きな荷重(図−4.14参照)を受けたことが
あり、現在は浸食その他の理由で、それが取り除かれた状態にある土がある。
このような土は過圧密、または先行圧密(4.4.2参照)を受けた土と呼ん
でいる。
過圧密を受けた土は、除荷の後、土の弾性によって幾分の変形回復がある
から、圧密の沈下計算においては、その影響を考えにいれなければならない。
すなわち、

また、粘土でも有機物を非常に多く含有している土は、その構造の特性の
ため、必ずしも乱さない正規圧密の粘土と同じように扱うことはできないと
考えられている。たとえば、泥炭性軟弱層では、沈下曲線が圧密理論と一致
せず、また沈下が長期にわたって継続するなど、やはり圧密試験の結果、そ
の特性を把握して処理する必要がある。
いうまでもないことであるが、一般に砂は透水性もよく、構造も簡単であ
るから、荷重を加えると短時間に圧縮が完了する。したがって、圧密荷関す
る問題は比較的少ないものと考えてよい。
|
 |
|
|
[ ↑目次へ戻る ]
|
 |
